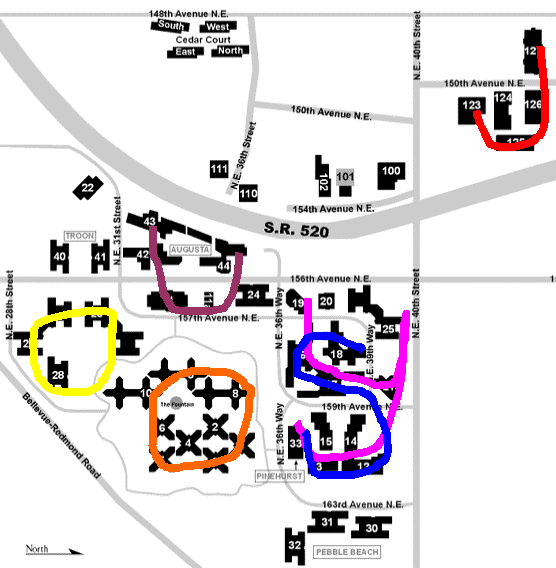
Dots Puzzle – Answer: JOYOUS
– By Eric LeVine
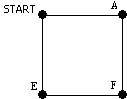The
first step in solving this puzzle is to correctly compute the values of each of
the intersections. There is actually a simple trick—the value of each
intersection is the sum of the values of the two prior intersections. For
example, there is only 1 way to get to A and 1 way to get to E. Therefore,
there are only 2 ways to get to F. Following this pattern across the entire map
yields the following values:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
Л |
Є |
Ф |
И |
Ђ |
Ж |
Ш |
|
1 |
1 |
1 |
1 |
1 |
2 |
3 |
4 |
5 |
5 |
2 |
5 |
9 |
14 |
19 |
19 |
5 |
14 |
28 |
47 |
66 |
66 |
14 |
42 |
89 |
155 |
221 |
221 |
42 |
131 |
286 |
507 |
728 |
The next step is to compute the provided formulae. A common mistake is to misinterpret the dot character (·) as a multiplication symbol. However, one formula has an asterisk (*) and that is clearly the symbol for multiplication. Correctly doing the math yields the following results:
127·126·125·123
8·3·5·10·9·8
19·16·17·21·25·21·12·13·33
26·28·27·26
44·11·42·43
18·16·17·14·13·33
The final leap is to connect the dots over a map of the Microsoft campus, tracing the letters to the solution. This spells JOYOUS.
